String Problem, Think Different
String Length Problem¶
- A string is wound symmetrically around a cylinder.
- The string goes exactly 4 times around the cylinder.
- The cylinder has a circumference of 4 and a length of 12.
What is the length of the string (Without using Calculus)?
In case you’re a math wizard, and know a bit about calculus, you can solve it using the arc length formula like so:
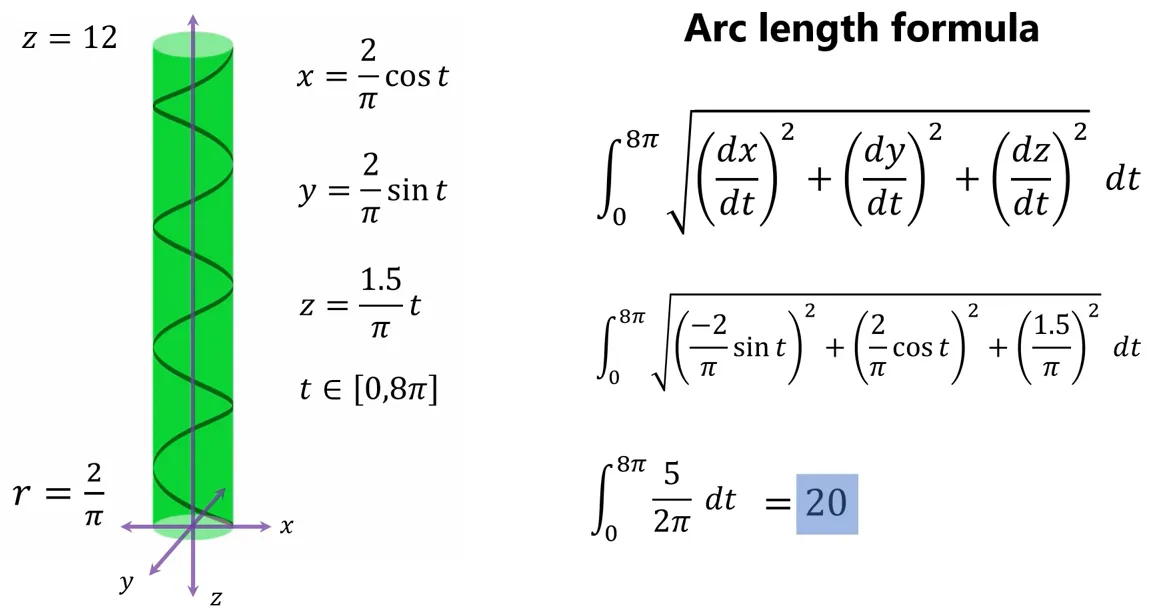 However, sometimes (often times), you just need to think a bit differently. BE a CONTRARIAN and find the solution!
However, sometimes (often times), you just need to think a bit differently. BE a CONTRARIAN and find the solution!
Contrarian Solution
To start the contrarian solution, imagine that the cylinder is a hollow toilet paper roll with the string glued in place, so that you can cut vertically as shown by the yellow line below. This means the string will be cut as well!
 Now, imagine flattening out the cut toilet paper roll so that the it forms a rectangle and the string simply becomes lines sub-dividing the rectangle as depicted below:
Now, imagine flattening out the cut toilet paper roll so that the it forms a rectangle and the string simply becomes lines sub-dividing the rectangle as depicted below:
 Is this problem easier to solve? ABSOLUTELY!
Is this problem easier to solve? ABSOLUTELY!
Now all we have to do is find the length of 1 part of the string and multiply it by 4, and since we know the cylinder circumference is 4, the short flat edge is also 4. We also know the height is 12 and the string divides 12 into 4 equal parts, making the other side of the triangle 3. Thus, we have a 3-4-5 triangle, so each line segment is 5 in length. So what is 5 units * 4 lengths? 20!!! The same as our overly complex calculus solution!
This is a case of learning to THINK DIFFERENT!
