Room Route

Graph Challenge

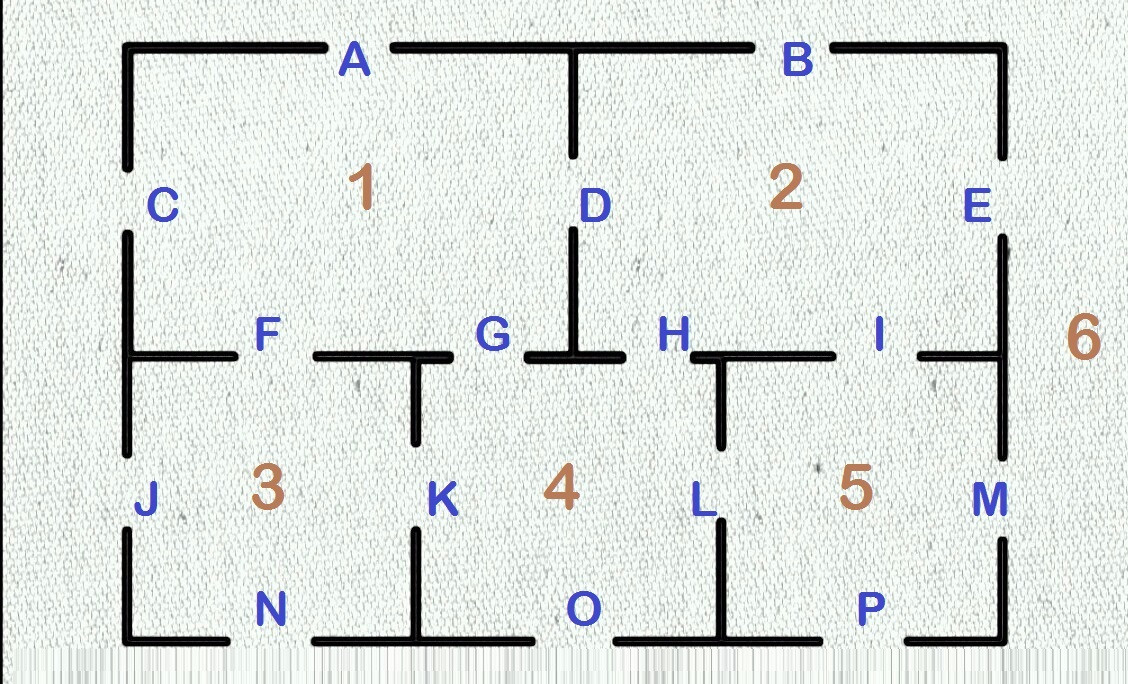
Given the following diagram of a house, can you find a path such that you will visit each room and can walk through every door exactly once, ending at the same starting door?

ANSWER

According to graph theory, Given a graph G, it is possible to find a walk that traverses each line exactly once, goes through all nodes, and ends at the starting point if all graph nodes have even degrees (or an even number of edges entering the node). This type of graph is known as a Eulerian Graph and this is the theorem:

Theorem: The following statements are equivalent for a connected graph G: 1. G is eulerian. 2. Every point of G has even degree.

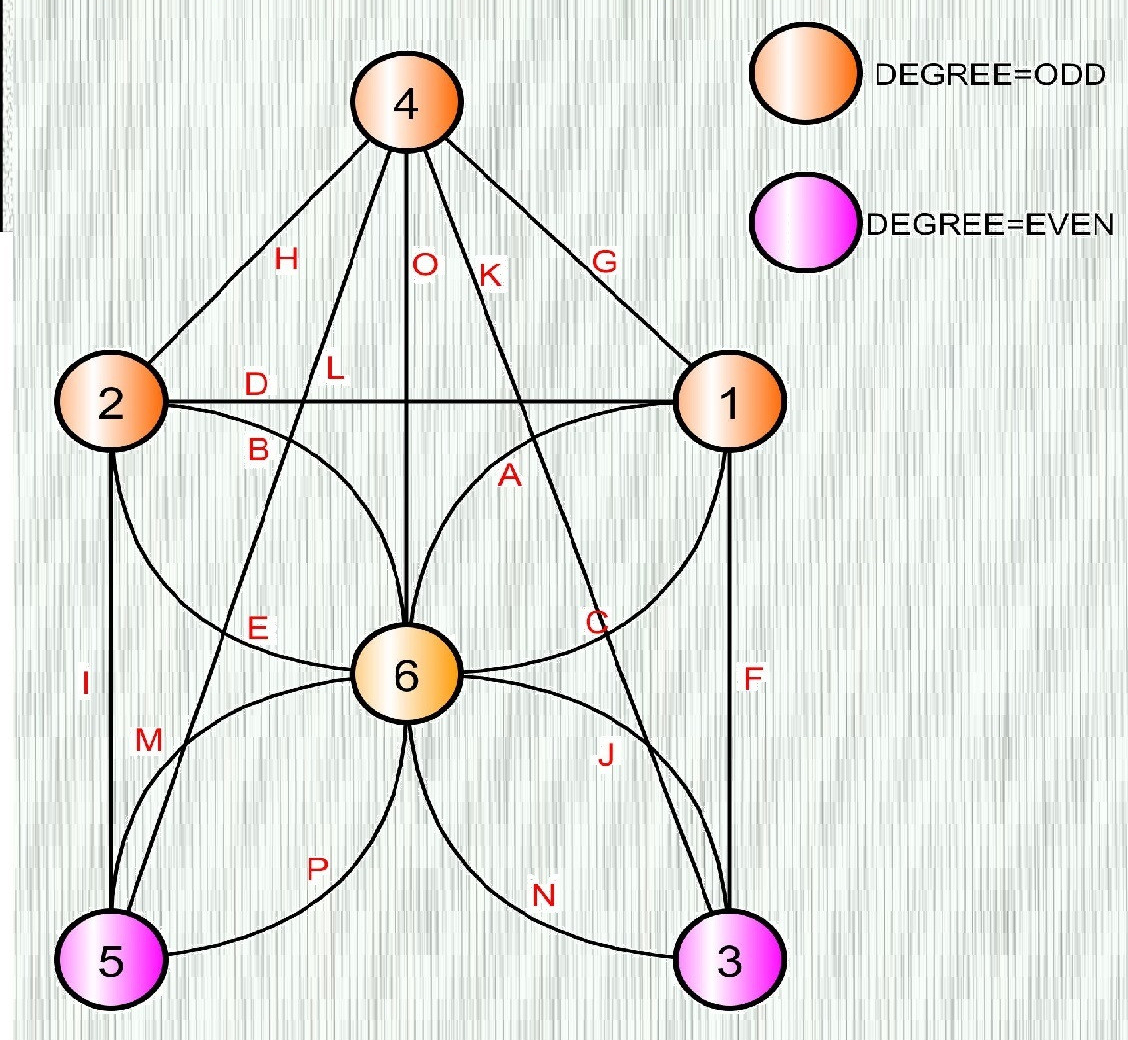
In this problem, if we assume each graph node is a Room (i.e. {1,2,3,4,5,6}), and each node is connected via edges that are the doors (i.e. {A,B,C,D,E,F,G,H,I,J,K,L,M,N,O,P}), we can build a graph as depicted below:

Now, since there are 4 nodes (i.e. rooms) that have an ODD degree (i.e. the number of edges/doors entering the node), by our Theorem, the graph is NOT Eulerian, and therefore can not be traversed in such a way that each node can be visited with each edge being traversed only once.

Thus, the solution is: There is no solution

Alternatively, you could solve this problem using recursion with memoization (i.e. door object property to lock the door) to traverse ALL possible routes and discover none of them work. Here is some sample code: Sample Recursive Code Proving there is no solution