Potato Cannon

Calculating Muzzle Velocity Using a Potato Cannon’s Trajectory and Range¶

Take Potato Ballistic Science With YOU!

Abstract¶

This project investigates the use of trajectory and range to determine the muzzle velocity of a potato gun. By measuring how far a potato travels and at what angle it’s launched, the muzzle velocity can be calculated. This project combines physics and engineering principles to understand projectile motion.

Question¶

How can the trajectory and range of a potato gun be used to accurately (minus some variables) calculate its muzzle velocity?

Hypothesis¶

If the launch angle and range of a potato gun are measured accurately, then the muzzle velocity can be calculated using projectile motion formulas, assuming air resistance is negligible.

Background Research¶

Research topics include:

Newton’s laws of motion
Projectile motion equations
Factors affecting muzzle velocity such as barrel length, friction, and angle of launch

Similar research in ballistics provides a foundation for calculating initial velocity based on projectile trajectory. I derive the equation this science project will need below!!!

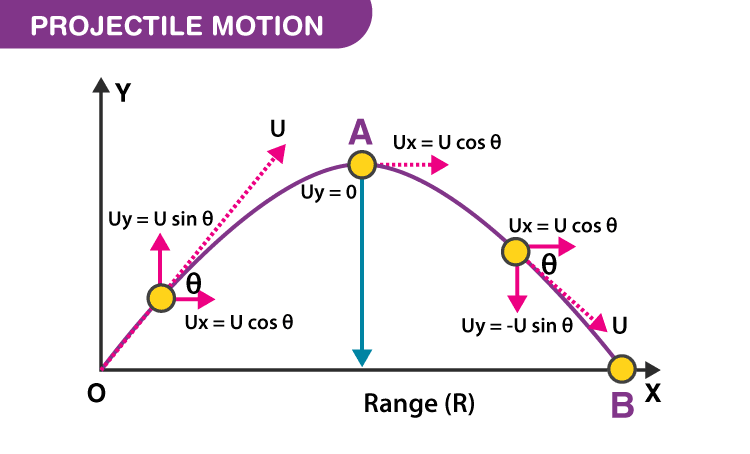
For a projectile launched with an muzzle velocity \( v \) at an angle \( \theta \) above the horizontal, we can break down the motion into horizontal (x) and vertical (y) components.

Initial Velocity Components¶

The initial velocity \( v \) can be split into:

Horizontal Component: \( v_x = v \cos \theta \)
Vertical Component: \( v_y = v \sin \theta \)

Calculate the Time of Flight¶

So, to find the range \( R \), horizontal distance traveled, we need the total time of flight (i.e. how long the potatoe stays in the air).

In projectile motion, the only vertical force acting on the object is gravity, which decelerates the object as it rises and accelerates it as it falls. When the projectile reaches its highest point (A), its vertical velocity is 0 (zero).

The vertical motion formula \( v_{y,\text{final}} = v_{y,\text{initial}} - g t \) (where \( g \) is the acceleration due to gravity, taken as 32.2 ft/s² on Earth), the time to reach the peak, \( t_{\text{up}} \), is:

\[ t_{\text{up}} = \frac{v_y}{g} = \frac{v \sin \theta}{g} \]

How did we get this?
- Without deriving the vertical motion formula, it intuitively makes sense that gravity over time would decelerate the initial velocity in the y direction, hence \( v_{y,\text{final}} = v_{y,\text{initial}} - g t \)
- \( v_{y,\text{final}} \) is 0 at \( t_{\text{up}} \)
- So, we simply made \( v_{y,\text{final}} \) 0, moved \( g t \) like so \( g t = v_{y,\text{initial}} \)
- Divided by \( g \) and substituted \( v_{y,\text{initial}} \) with its equivalent \( v \sin \theta \)

Since the time to go up equals the time to come down, the total time of flight, \( t_{\text{total}} \), is:

\[ t_{\text{total}} = 2 \cdot t_{\text{up}} = 2 \cdot \frac{v \sin \theta}{g} = \frac{2 v \sin \theta}{g} \]

Calculate the Range¶

The horizontal motion is unaffected by gravity (assuming no air resistance), so the horizontal velocity \( v_x \) remains constant at \( v \cos \theta \). The range \( R \) is the horizontal distance traveled in the total time of flight:

\[ R = v_x \cdot t_{\text{total}} = (v \cos \theta) \cdot \frac{2 v \sin \theta}{g} \]

Remember the famous \( rate \times time = distance \) formula you likely were forced to memorize!

Simplify Using Trigonometric Identity¶

Using the trigonometric identity \( 2 \sin \theta \cos \theta = \sin(2 \theta) \), we can simplify:

\[ R = \frac{v^2 \sin(2 \theta)}{g} \]

This formula is FULL of assassumptions, but I’m gonna be lazy and assume:

The only force acting on the projectile is gravity.
The launch and landing heights are the same.
Air resistance is negligible.

Finding Muzzle Velocity¶

The above formula can be used to find the muzzle velocity if you know the range \( R \) and launch angle \( \theta \)!

Materials¶

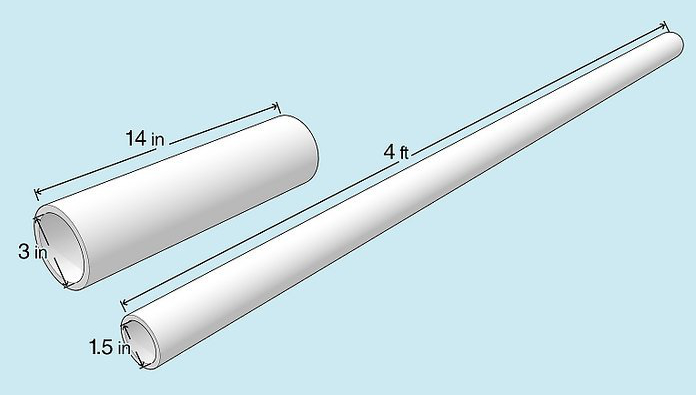
Potato gun with a 1.5-inch diameter ABS barrel (48 inches long) and a 14-inch chamber (~ 3.5-inch diameter)
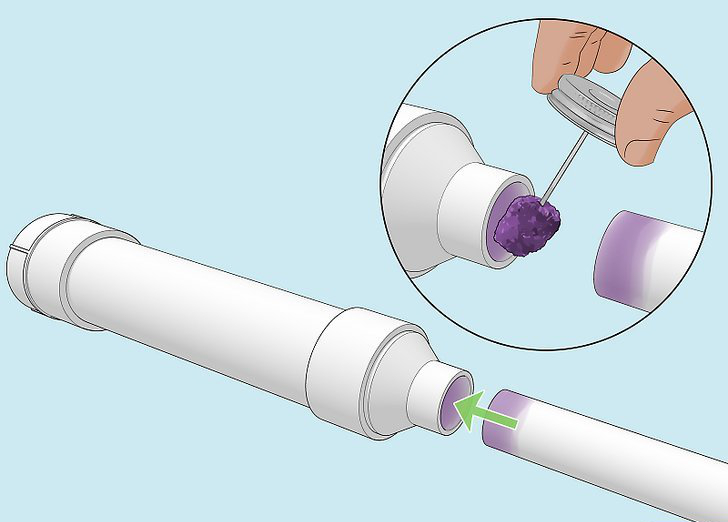
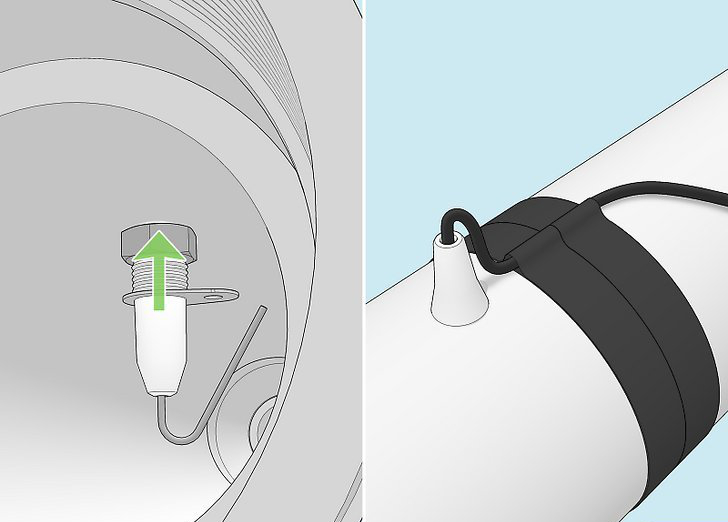
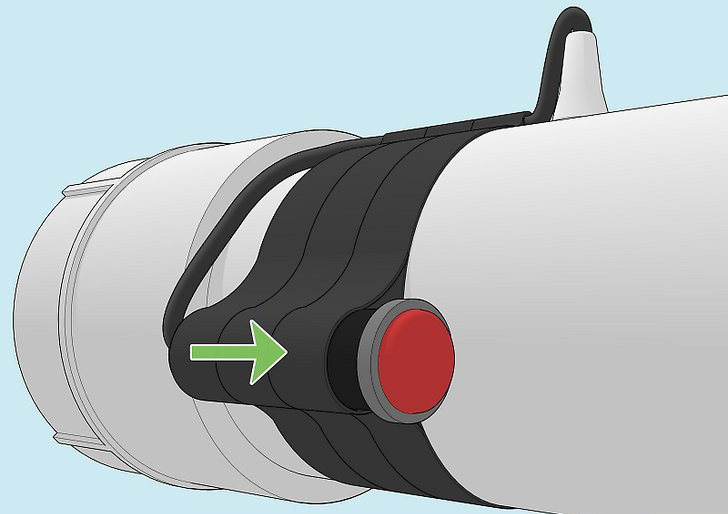
Potatoes (as projectiles)
Protractor or inclinometer for measuring launch angle
Tape measure or laser distance measurer
Calculator or computer with software for trajectory calculations
Safety goggles and ear protection

Procedure¶

Setup and Safety: Set up the testing area with clear sight lines and secure zones. Used protective equipment.
Launch Angle: Used the protractor to set and measure a specific launch angle.
Measurement: Fired the potato gun, and recorded the range (distance from launch point to landing point).
Data Collection: Repeated for different angles and record each range.
Calculations: Used the range and angle data with projectile motion equations to calculate initial velocity (muzzle velocity).

Results¶

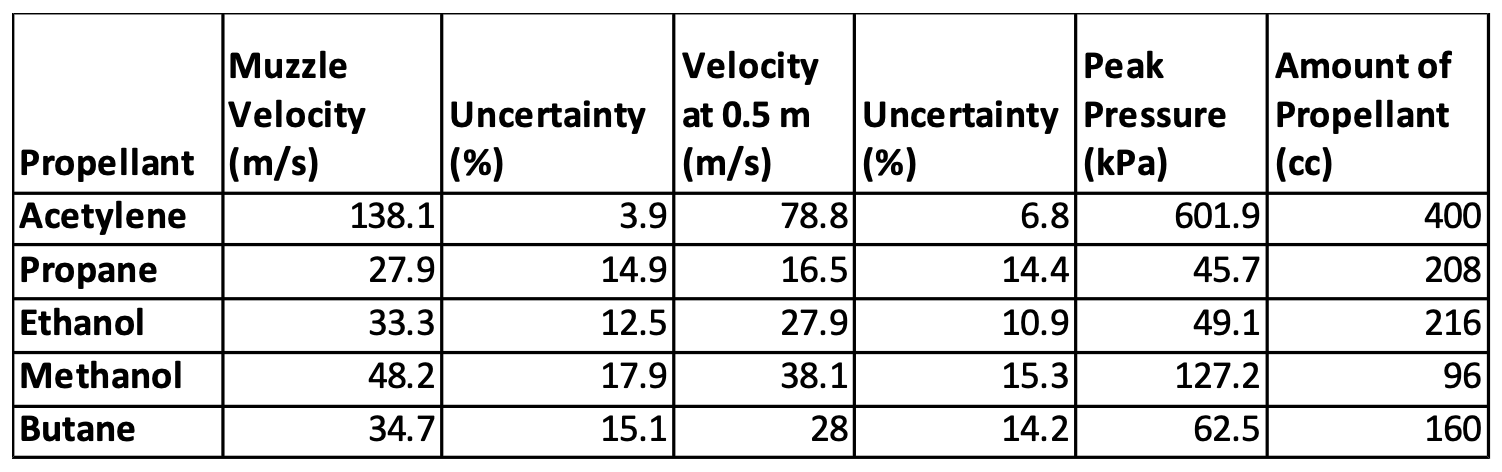
TODO: Need to add formatted table results
Calculating muzzle velocity using the projectile motion formula for Range

\[ R = \frac{v^2 \sin(2\theta)}{g} \]

where:

\( R \) is the range in feet,
\( v \) is the muzzle velocity we want to find,
\( \theta \) is the launch angle, and
\( g \) is the acceleration due to gravity (32.2 ft/s²).

Muzzle Velocity Calculation¶

if:

\( R \) is 200 yards, about 600 feet
\( \theta \) is an angle of 45 degrees
\( g \) is the acceleration due to gravity (32.2 ft/s²).

Then \(\sin(2 \times 45^\circ) = 1\), the formula simplifies to:

\[ R = \frac{v^2}{g} \]

Rearranging to solve for \( v \):

\[ v = \sqrt{R \times g} \]

\[ v = \sqrt{600 \times 32.2} \]

\[ v = \sqrt{19320} \approx 139 \text{ ft/s} \]

So, the muzzle velocity is approximately 139 feet per second in this scenario.

Experiements by the USAF Academy in a paper “Studying the Internal Ballistics of a Combustion Driven Potato Cannon using High-speed Video appear to correllate with these calculations.

Conclusion¶

The calculated muzzle velocities for my various firing attempts were between 91 ft/s (62 mph) and 150 ft/s (107 mph) which varied both with the angle of the gun and with the quantity of propellant used, though the propellant had a larger effect. The angle affected range significantly, but didn’t appear to greatly impact muzzle velocity. In the calculation shown above, an angle of about 45 degrees produced the greatest ranges, but not the greatest muzzle velocities, though I need more experimental data to determine if that’s a valid observation. All calculated muzzle velocities do corroborate other experimental evidence on the muzzle velocity of potato guns, so my hypothesis is supported, that having the angle and range allows you to accurately predict muzzle velocity.

Future Direction¶

Investigate the effects of varying potato mass, air pressure, or chamber volume on muzzle velocity.
Explore using high-speed cameras to calculate velocity directly and compare with trajectory-based calculations.
Determine if audio from a potato exiting the muzzle and hitting a gong can be used to calculate muzzle velocity.